模型的右邊是端口2，該端口也會產生一個不希望出現的小互調能量，以IM2表示。所有用于端口1的假設同樣適用于端口2。通觀完整的集成電纜無源互調的測量模型，以下幾條值得關注：

每個測試端口都有與其相關的4個互調響應。其中兩個是接頭末端產生的，另兩個是互調分析儀自身產物。

電纜b端的互調（IMb）和端口2的互調（IM2）會通過電纜反向傳輸，從而產生的反射互調響應可以在端口1處測量。

電纜a端的互調（IMa）和端口1的互調（IM1）會通過電纜進行傳輸，從而產生的通過互調響應可以在端口2處測量。

通過這個模型，集成電纜的互調值就可以被確定了。

四、使用模型預計互調特性

雖然預計一個給定的射頻器件的互調絕對值是非常困難的，但是單個互調源之間的相互作用在圖2的模型中可以很容易地被表現出來。

首先，我們已經知道了每一個互調源的三階互調公式。以端口1和電纜a端的響應開始，互調響應為：

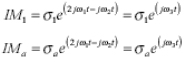
三階互調的頻率為：
w₃ ≡2ω₂ −ω₁

其中
t：時間
IM1：端口1的三階互調響應
IMa：電纜a端的三階互調響應
σ₁：端口1的互調系數，即端口1(=10^[dBc/20.])的dBc響應的簡單數字轉化
σ_a：端口a的互調系數，即端口a(=10^[dBc/20.])的dBc響應的簡單數字轉化
ω_{1, 2, 3}：分別為載波1，載波2和產生的三階互調響應的頻率弧度

電纜b端和端口2的互調響應相對稍微復雜。兩個載波產生的互調響應可以通過電纜傳輸函數H(w)表示。為了簡化公式，和消除非線性功率對互調產物及其載波的影響，假設電纜是無損耗的。在公式中，這個假設表示為：
|H(w) |= 1

當最終結果出來時，這個假設對于模型精確度的影響是非常顯著的。

即使假設電纜是無損耗的，電纜產生的群時延還是被包含在模型中的，具體如下式：

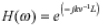
其中：
k：與頻率有關的通過電纜(2p/l)的電磁波數
v：同軸電纜的傳輸速率
L：電纜的長度

電纜b端和端口2的互調響應表示為：

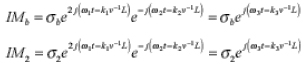
當公式中IMa、IM1、IMb、和IM2已知，落在端口2上，總的通過（前向）互調表達式為：

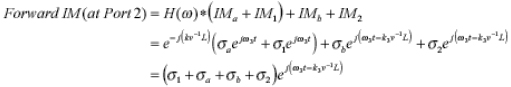
上式表示同時落在互調測試設備端口2上的四個互調響應，不依賴于互調頻率。假設單獨的互調源是不依賴于頻率的，且電纜的損耗是一個常數，那么整條集成電纜的通過互調響應將不依賴于頻率。

我們可以采用相似的過程來描述反射互調響應。反射互調響應可以由下式來給出：
Reflected IM at Port ( 1) = IM_a + IM₁ + H(w)∗(IM_b + IM₂ )

簡化為：

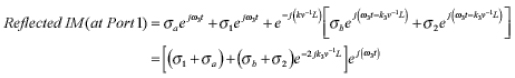
上式表示端口1中的反射互調響應是端口1和電纜b端響應的合成，加上由于電纜b端和端口2的互調響應的合成造成的移相響應。由于存在一個不同相位的互調源的合成向量，所以，我們認為反射互調響應是一個與電纜的頻率和電長度有關的函數。

五、集成電纜互調響應的測量

為了驗證該模型，我們使用SI-1900A型無源互調失真分析儀來測量無線通信應用中一種典型的集成跳線。該集成跳線長1.5米，廠商標注的速率因子為82%，兩端分別安裝有一個DIN-M型接頭。載波功率設置為20W/路。分析儀的自適應邏輯電路確保了測試過程中，載波的功率變化不超過0.2dB。分析儀的底噪不超過-140dBm，即當施加一個+43dBm的載波功率時，分析儀的互調底噪不超過-163dBc。

圖3顯示了反射和通過互調響應的測量結果曲線，以及相應的預測曲線。電纜每個端口上的互調響應值，是通過假設前向互調響應是由兩個分別在電纜兩端的等幅互調源之和組成的。反射互調響應值僅由該模型來決定，且不用調節使之與測得的數據相匹配。